Números de la suerte

¿Quién no se acuerda de la criba de Eratóstenes para obtener los números primos?

Primero se tachaban todos los múltiplos de 2, dejando el 2. 

Luego se tachaban los múltiplos de 3, salvo el 3.

El siguiente que encontramos sin tachar es el 5, así que tachamos todos sus múltiplos.

Continuamos con los múltiplos de 7, de 11... Y obtenemos una tabla en la que quedan exclusivamente  el 1 y los números primos. 

Pues bien, en 1955 Stanislaw Ulam, miembro de la legendaria escuela polaca de matemáticas, (hay una preciosa autobiografía titulada Aventuras de un matemático, publicado por Ed. Nivola),  se le ocurrió tachar los números de otra forma:

- Tachamos el 2 y todos sus múltiplos. Nos quedan: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21...

- Tras el 1, el siguiente número de la lista es el 3. Tachamos, de los que quedaban, uno de cada tres, el tercero exactamente. Y nos quedan: 1, 3, 7, 9, 13, 15, 19, 21...

Tras el 1 y el 3, el siguiente sobreviviente es el 7, así que tachamos, uno de cada siete, el séptimo. Nos quedan: 1, 3, 7, 9, 13, 15, 21...

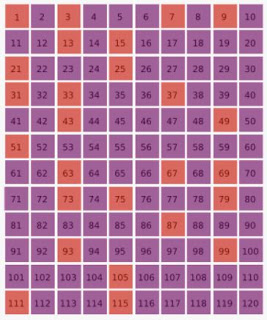
La criba de Ulam nos queda así: 

Los números de las casillas naranjas son los números de la suerte.

Si hasta ahora nunca te ha tocado un premio sustancioso de la Primitiva, prueba a jugar sólo con estos números... ¡seguirás igual de pobre casi seguro! Pero si te haces millonario acuérdate de mi.

Lo curioso del caso es que estos números tienen muchas propiedades comunes con los números primos. Son infinitos, eso está demostrado. Lo que no sabemos aún es si cumplen el equivalente a la conjetura de Golbach: "Todo número par es la suma de dos números de la suerte"

No son cuestiones baladíes. Hasta Martín Gardner mostró su interés por ellos en 1997 en la revista The Mathematical intelligencer.